Backtracking Algorithm

In this blog we will discuss another problem solving strategy known as Backtracking. Backtracking is in a way similar to brute force paradigm to solve a problem but has some optimisations which make it better than vanilla brute force algorithms.

Backtracking problems generally have many possible solutions and the intention is to find them all. Backtracking is recursive where we incrementally builds candidates of a solution set and abandon a candidate as soon as we realise that this candidate will not result in a valid solution

Etymology

Generally in backtracking problems have many possible solutions. To find all these solutions, we incrementally builds one solution at a time. At each step while building a possible solution we check if it satisfies the constraints of the given problem. If a solution satisfies the constraint we add it to the final solution set else we move back from the current state to try other possible solutions. This is an optimisation over plain brute force as we stop building a solution at the point of the first constraint violation.

Bounding function

Bounding function is a function which we use to check if a possible solution satisfy the constraints of the given problem.

State Space Tree

State Space tree represents all the possibilities which we try in a backtracking problem. This helps us in visualise the possibilities which we are trying and how the algorithm is moving backwards in case of constraint violations.

We start from the root of the tree and start taking steps towards finding a solution. At each step we check if the current step satisfy the problem. If yes we keep moving forward to find the solution. If the constraint fails we remove the intermediate state to find other possibilities.

I will try to explain this using a very simple example.

Problem

Say suppose we have three chairs and we have three students A, B and C. We need to find all the possible ways in which these students can sit on these chairs provided that C is not sitting on the middle chair.

Solution

• Start by placing one of the student on the first chair.
• Once done now place the next student on the next chair.
• Check if C is sitting on the second chair.
  • If YES, then we have violated the constraint (represented by red nodes in our state space tree).
    • Since the constraint is already violated we will not go ahead and place the remaining child on the third chair.
    • Rather we will remove the current intermediate state from the list of possible solution and try to find other possibilities
  • If NO, then go ahead and place the remaining student on the third chair
    • Great! we have found a possible solution and this can be added to our final list of possibilities

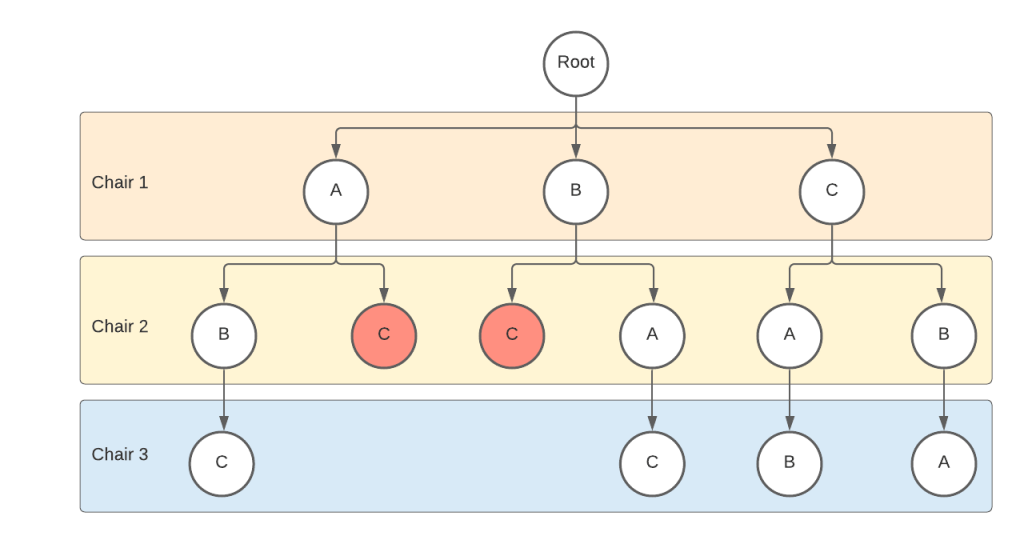
Hence by following the above algorithm, the final list of possibilities will be as below

[ [A, B, C], [B, A, C], [C, A, B], [C, B, A]]

Next Steps

I hope this will serve as a good starting point in your journey to master backtracking algorithm. As with any programming methodology the more you practice the more things get clear. Please read more about some standard backtracking problems like N-Queen, Sudoku solver etc to get more insights on how backtracking actually works.

Please do let me know in case you need any more information or in case you have any questions.